Calculo Diferencial: junio 2012

La transformada de Laplace recibe su nombre en honor del matemático francés Pierre-Simon Laplace, que la presentó dentro de su teoría de la probabilidad. En 1744, Leonhard Euler había investigado un conjunto de integrales de la forma:

$z = \int X(x) e^{ax}\, dx$

$z = \int X(x) x^A \, dx$

— como soluciones de ecuaciones diferenciales, pero no profundizó en ellas y pronto abandonó su investigación. Joseph Louis Lagrange, admirador de Euler, también investigó ese tipo de integrales, y las ligó a la teoría de la probabilidad en un trabajo sobre funciones de densidad de probabilidad de la forma:

$\int X(x) e^{- a x } a^x\, dx,$

— que algunos historiadores interpretan como auténticas transformadas de Laplace.

Este tipo de integrales atrajeron la atención de Laplace cuando, en 1782, y siguiendo la idea de Euler, trató de emplear estas integrales como soluciones de ecuaciones diferenciales. Parece ser que en 1785 dio un paso más allá, y reenfocó el problema para en vez de usar las integrales como soluciones, aplicarlas a las ecuaciones dando lugar a las transformadas de Laplace tal y como hoy en día se entienden. Usó una integral de la forma:

$\int x^s \phi (s)\, dx,$

— análoga a la transformada de Mellin, con la que transformó una ecuación diferencial en una ecuación algebraica de la que buscó su solución. Planteó alguna de las principales propiedades de su transformada, y de alguna forma reconoció que el método de Joseph Fourier para resolver por medio de series de Fourier la ecuación de difusión podría relacionarse con su transformada integral para un espacio finito con soluciones periódicas.

Pese al logro, las transformadas de Laplace pronto cayeron en un relativo olvido, al haber sido presentadas en el campo de la probabilidad –ajeno a su moderna aplicación en la física y la ingeniería–, y ser tratadas sobre todo como objetos matemáticos meramente teóricos.

La moderna aplicación de las transformadas de Laplace y toda su teoría subyaciente surge en realidad en la segunda mitad del siglo XIX. Al tratar de resolver ecuaciones diferenciales relacionadas con la teoría de vibraciones, el ingeniero inglés Oliver Heaviside (1850-1925) descubrió que los operadores diferenciales podían tratarse analíticamente como variables algebraicas. De acuerdo con el "cálculo operacional", si se tiene una ecuación diferencial de la forma:

$(D-a)y=f(t)\,$

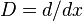— donde D es el operador diferencial, esto es, $D=d/dx$ , entonces la solución general a dicha ecuación es de la forma:

$y=e^{at} \int e^{-at} f(t) dt +c_1 e^{at}$ .

Heaviside observó que si se trataba al operador D como una variable algebraica, era posible alcanzar igualmente la solución de toda ecuación pareja a la de arriba. En efecto, según la solución general, se cumple que:

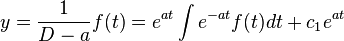
$y=\frac 1 {D-a} f(t)= e^{at} \int e^{-at} f(t) dt +c_1 e^{at}$

Entonces, si se considera una ecuación diferencial de segundo orden como la siguiente:

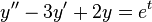
$y''-3y'+2y=e^t\,$

— ésta puede reescribirse en para resaltar el operador D como:

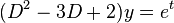
$(D^2-3D+2)y=e^t\,$

Heaviside propuso despejar y y tratar a D algebraicamente, en cuyo caso se tendría que:

$y= \frac {e^t} {D^2-3D+2} = \frac {e^t} {(D-1)(D-2)}=\frac 1 {D-2} e^t - \frac 1 {D-1} e^t$

Sustituyendo las fracciones en D por la expresión integral de las mismas arriba presentada, se llega a la solución de la ecuación diferencial:

$y=(e^{2t} \int e^{-2t} f(t) dt +c_1 e^{2t})-(e^{t} \int e^{-t} f(t) dt +c_2 e^{t})=e^{2t}(-e^{-t})+c_1 e^{2t})-(e^t (t) +c_2 e^t)$

$\Big (y=c_1 e^{2t}- (c_2+1) e^t -t e^t \Big)$

Heaviside publicó sus resultados, cuya utilidad a la hora de resolver ecuaciones de la física y la ingeniería hizo que pronto se extendieran. Sin embargo, el trabajo de Heaviside, formal y poco riguroso, atrajo las críticas de algunos matemáticos puristas que los rechazaron argumentando que los resultados de Heaviside no podían surgir de tal forma. No obstante, el éxito del método hizo que pronto fuera adoptado por ingenieros y físicos de todo el mundo, de manera que al final atrajo la atención de cierto número de matemáticos tratando de justificar el método de manera rigurosa. Tras varias décadas de intentos, se descubrió que la Transformada descubierta por Laplace hacía un siglo no sólo ofrecía un fundamento teórico al método de cálculo operacional de Heaviside, sino que además ofrecía una alternativa mucho más sistemática a tales métodos.

Hacia principios del siglo XX, la transformada de Laplace se convirtió en una herramienta común de la teoría de vibraciones y de la teoría de circuitos, dos de los campos donde ha sido aplicada con más éxito. En general, la transformada es adecuada para resolver sistemas de ecuaciones diferenciales lineales con condiciones iniciales en el origen. Una de sus ventajas más significativas radica en que la integración y derivación se convierten en multiplicación y división. Esto transforma las ecuaciones diferenciales e integrales en ecuaciones polinómicas, mucho más fáciles de resolver.También se aplica en EDP y ecuaciones diferenciales en diferencias.

[editar]Propiedades

[editar]Linealidad

$\mathcal{L}\left\{a f(t) + b g(t) \right\} = a \mathcal{L}\left\{ f(t) \right\} + b \mathcal{L}\left\{ g(t) \right\}$

[editar]Derivación

$\mathcal{L}\{f'(t)\} = s \mathcal{L}\{f(t)\} - f(0)$

$\mathcal{L}\{f''(t)\} = s^2 \mathcal{L}\{f(t)\} - s f(0) - f'(0)$

$\mathcal{L}\left\{ f^{(n)}(t) \right\} = s^n \mathcal{L}\{f(t)\} - s^{n - 1} f(0) - \cdots - f^{(n - 1)}(0)$ =

= $\mathcal{L}\left\{ f^{(n)}(t) \right\} = s^n \mathcal{L}\{f(t)\} - \sum_{i=1}^{n} s^{n - i} f^{(i - 1)}(0)$

[editar]Integración

$\mathcal{L}\left\{ \int_0^t f(\tau)\, d\tau \right\} = {1 \over s} \mathcal{L}\{f\}$

[editar]Dualidad

$\mathcal{L}\{ t f(t)\} = -F'(s)$

[editar]Desplazamiento de la frecuencia

$\mathcal{L}\left\{ e^{at} f(t) \right\} = F(s-a)$

Desplazamiento temporal

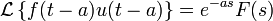
$\mathcal{L}\left\{ f(t - a) u(t - a) \right\} = e^{-as} F(s)$

$\mathcal{L}^{-1} \left\{ e^{-as} F(s) \right\} = f(t - a) u(t - a)$

Nota: $u(t)$ es la función escalón unitario.

[editar]Desplazamiento potencia n-ésima

$\mathcal{L}\{\,t^nf(t)\} = (-1)^nD_s^n[F(s)]$

[editar]Convolución

$\mathcal{L}\{f*g\} = \mathcal{L}\{ f \} \mathcal{L}\{ g \}$

[editar]Transformada de Laplace de una función con periodo p

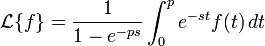
$\mathcal{L}\{ f \} = {1 \over 1 - e^{-ps}} \int_0^p e^{-st} f(t)\,dt$

[editar]Condiciones de convergencia

$\mathcal{L}\{(e^{t^2})\}$ (que crece más rápido que $e^{-st}$ ) no pueden ser obtenidas por Laplace, ya que $e^{t^2}$ , es una función de orden exponencial de ángulos.

[editar]Teorema del valor inicial

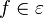Sea una función $f\in\varepsilon$ derivable a trozos y que $f^{\prime}\in\varepsilon.$ Entonces :

$f(0^{+})=\lim_{s\to\infty}{sF(s)}$

$\varepsilon$ es el conjunto de funciones continuas a trozos con orden exponencial.

[editar]Teorema del valor fina

Sea $f\in\varepsilon$ una función derivable a trozos tal que $f^{\prime}\in\varepsilon$ .Entonces :

$f(\infty)=\lim_{s\to0}{sF(s)}$

$\varepsilon$ es el conjunto de funciones continuas a trozos con orden exponencial.

Tabla de las transformadas de Laplace más comunes

La siguiente tabla provee la mayoría de las transformaciones de Laplace para funciones de una sola variable.

Debido a que la transformada de Laplace es un operador lineal, la transformada de Laplace de una suma es la suma de la transformada de Laplace de cada término

$\mathcal{L}\left\{f(t) + g(t) \right\} = \mathcal{L}\left\{f(t)\right\} + \mathcal{L}\left\{ g(t) \right\}$

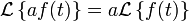
$\mathcal{L}\left\{a f(t)\right\} = a \mathcal{L}\left\{ f(t)\right\}$

Aquí está una lista de las transformadas más comunes. En ella $u$ denota a la llamada función de Heaviside o función escalón, que vale 1 cuando su argumento es positivo y 0 cuando su argumento es negativo. Cuando su argumento vale 0 se le suele asignar el valor 1/2, aunque esto no tiene relevancia práctica.

Función

Dominio en el tiempo
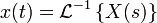
$x(t) = \mathcal{L}^{-1} \left\{ X(s) \right\}$

Dominio en la frecuencia
$X(s) = \mathcal{L}\left\{ x(t) \right\}$

Región de la convergencia
para sistemas causales

retaso ideal

$\delta(t-\tau) \$

$e^{-\tau s} \$

impulso unitario

$\delta(t) \$

$1 \$

$\mathrm{todo} \ s \,$

enésima potencia retrasada y con
desplazamiento en la frecuencia

$\frac{(t-\tau)^n}{n!} e^{-\alpha (t-\tau)} \cdot u(t-\tau)$

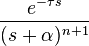
$\frac{e^{-\tau s}}{(s+\alpha)^{n+1}}$

$s > - \alpha \,$

n-ésima potencia

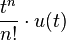
${ t^n \over n! } \cdot u(t)$

${ 1 \over s^{n+1} }$

$s > 0 \,$

2a.1

q-ésima potencia

${ t^q \over \Gamma(q+1) } \cdot u(t)$

${ 1 \over s^{q+1} }$

$s > 0 \,$

2a.2

escalón unitario

$u(t) \$

${ 1 \over s }$

$s > 0 \,$

escalón unitario con retraso

$u(t-\tau) \$

${ e^{-\tau s} \over s }$

$s > 0 \,$

Rampa

$t \cdot u(t)\$

$\frac{1}{s^2}$

$s > 0 \,$

potencia n-ésima con cambio de frecuencia

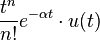
$\frac{t^{n}}{n!}e^{-\alpha t} \cdot u(t)$

$\frac{1}{(s+\alpha)^{n+1}}$

$s > - \alpha \,$

2d.1

amortiguación exponencial

$e^{-\alpha t} \cdot u(t) \$

${ 1 \over s+\alpha }$

$s > - \alpha \$

convergencia exponencial

$( 1-e^{-\alpha t}) \cdot u(t) \$

$\frac{\alpha}{s(s+\alpha)}$

$s > 0\$

exponencial doble

$\frac{1}{b-a}\left(e^{-at}-e^{-bt}\right)$

$\frac{1}{(s+a)(s+b)}$

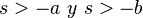
$s > -a \ y \ s > -b\$

seno

$\sin(\omega t) \cdot u(t) \$

${ \omega \over s^2 + \omega^2 }$

$s > 0 \$

coseno

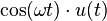
$\cos(\omega t) \cdot u(t) \$

${ s \over s^2 + \omega^2 }$

$s > 0 \$

Seno con fase

$\sin(\omega t+\varphi)\cdot u(t)$

$\frac{ s \sin(\varphi) + \omega\cos\varphi}{s^2+\omega^2}$

$s > 0 \$

seno hiperbólico

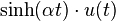
$\sinh(\alpha t) \cdot u(t) \$

${ \alpha \over s^2 - \alpha^2 }$

$s > | \alpha | \$

coseno hiperbólico

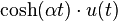
$\cosh(\alpha t) \cdot u(t) \$

${ s \over s^2 - \alpha^2 }$

$s > | \alpha | \$

onda senoidal con
amortiguamiento exponencial

$e^{-\alpha t} \sin(\omega t) \cdot u(t) \$

${ \omega \over (s+\alpha )^2 + \omega^2 }$

$s > -\alpha \$

onda cosenoidal con
amortiguamiento exponencial

$e^{-\alpha t} \cos(\omega t) \cdot u(t) \$

${ s+\alpha \over (s+\alpha )^2 + \omega^2 }$

$s > -\alpha \$

raíz n-ésima

$\sqrt[n]{t} \cdot u(t)$

$s^{-(n+1)/n} \cdot \Gamma\left(1+\frac{1}{t}\right)$

$s > 0 \,$

logaritmo natural

$\ln \left ( { t \over t_0 } \right ) \cdot u(t)$

$- { t_0 \over s} \ [ \ \ln(t_0 s)+\gamma \ ]$

$s > 0 \,$

Función de Bessel
de primer tipo,
de orden n

$J_n( \omega t) \cdot u(t)$

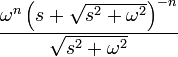
$\frac{ \omega^n \left(s+\sqrt{s^2+ \omega^2}\right)^{-n}}{\sqrt{s^2 + \omega^2}}$

$s > 0 \,$
$(n > -1) \,$

Función de Bessel modificada
de primer tipo,
de orden n

$I_n(\omega t) \cdot u(t)$

$\frac{ \omega^n \left(s+\sqrt{s^2-\omega^2}\right)^{-n}}{\sqrt{s^2-\omega^2}}$

$s > | \omega | \,$

Función de Bessel
de segundo tipo,
de orden 0

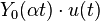
$Y_0(\alpha t) \cdot u(t)$

Función de Bessel modificada
de segundo tipo,
de orden 0

$K_0(\alpha t) \cdot u(t)$

Función de error

$\mathrm{erf}(t) \cdot u(t)$

${e^{s^2/4} \operatorname{erfc} \left(s/2\right) \over s}$

$s > 0 \,$

Notas explicativas:

$u(t) \,$ representa la función escalón unitario.
$\delta(t) \,$ representa la Delta de Dirac.
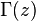$\Gamma (z) \,$ representa la función gamma.
$\gamma \,$ es la constante de Euler-Mascheroni.

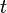$t \,$ , un número real, típicamente representa tiempo, aunque puede representarcualquier variable independiente.
$s \,$ es la frecuencia angular compleja.
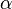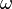$\alpha \,$ , $\beta \,$ , $\tau \,$ , y $\omega \,$ son números reales.
$n \,$ es un número entero.

Calculo Diferencial

martes, 26 de junio de 2012

4.3 Aplicaciones Sistemas de ecuaciones diferenciales lineales

4.2.2 Metodo Utilizando transformada de Laplace

[editar]Propiedades

[editar]Linealidad

[editar]Derivación

[editar]Integración

[editar]Dualidad

[editar]Desplazamiento de la frecuencia

Desplazamiento temporal

[editar]Desplazamiento potencia n-ésima

[editar]Convolución

[editar]Transformada de Laplace de una función con periodo p

[editar]Condiciones de convergencia

[editar]Teorema del valor inicial

[editar]Teorema del valor fina

Sea $f\in\varepsilon$ una función derivable a trozos tal que $f^{\prime}\in\varepsilon$ .Entonces :

Contribuyentes

Archivo del blog

martes, 26 de junio de 2012

4.3 Aplicaciones Sistemas de ecuaciones diferenciales lineales

4.2.2 Metodo Utilizando transformada de Laplace

[editar]Propiedades

[editar]Linealidad

[editar]Derivación

[editar]Integración

[editar]Dualidad

[editar]Desplazamiento de la frecuencia

Desplazamiento temporal

[editar]Desplazamiento potencia n-ésima

[editar]Convolución

[editar]Transformada de Laplace de una función con periodo p

[editar]Condiciones de convergencia

[editar]Teorema del valor inicial

[editar]Teorema del valor fina

Sea una función derivable a trozos tal que .Entonces :

Contribuyentes

Archivo del blog

Sea $f\in\varepsilon$ una función derivable a trozos tal que $f^{\prime}\in\varepsilon$ .Entonces :