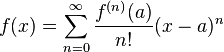viernes, 1 de julio de 2011
3.3 Cálculo de volúmenes sólidos de revolución
Si giramos una región del plano alrededor de un eje obtenemos un sólido de revolución. El más simple de ellos es el cilindro circular recto o disco, que se forma al girar un rectángulo alrededor de un eje adyacente a uno de los lados del rectángulo. El volumen de este disco de radio R y de anchura es:
Se trata de hallar el volumen de este cuerpo engendrado por R. Para ello hay que seguir un proceso similar al realizado en la definición de integral definida.
Elegimos una partición regular de [a, b]:
Estas divisiones determinan en el sólido n discos cuya suma se aproxima al volumen del mismo. Teniendo en cuenta que el volumen de un disco es , la suma de Riemann asociada a la partición, y que da un volumen aproximado del sólido es:
siendo:
Por tanto, recordando la definición de integral definida de Riemann se obtiene que:
Además, si se toma el eje de revolución verticalmente, se obtiene una fórmula similar:
2. Volúmenes de revolución: El Método de las arandelas
El método de los discos puede extenderse fácilmente para incluir sólidos de revolución con un agujero, reemplazando el disco representativo por una arandela representativa. La arandela se obtiene girando un rectángulo alrededor de un eje. Si R y r son los radios externos e internos de la arandela, y es la anchura de la arandela, entonces el volumen viene dado por:
Si las funciones se cortan, habrá que calcular los volúmenes de los sólidos engendrados en cada uno de los subintervalos donde se puede aplicar el método anterior.
3. Método de secciones conocidas
En este apartado veremos cómo se calcula el volumen de algunos cuerpos geométricos cuando conocemos el área de las bases de los cilindros parciales en que hemos dividido el sólido. Con el método de discos, podemos hallar el volumen de un sólido que tenga una sección circular cuya área sea A = R2. Podemos generalizar este método a sólidos de cualquier forma siempre y cuando sepamos la fórmula del área de una sección arbitraria, como cuadrados, rectángulos, triángulos, semicírculos y trapecios.
Consideremos un sólido que tiene la propiedad de que la sección transversal a una recta dada tiene área conocida. Esto equivale a decir intuitivamente que en cada corte que hacemos, conocemos el área de la sección correspondiente.
En particular, supongamos que la recta es el eje OX y que el área de la sección transversal está dada por la función A(x), definida y continua en [a,b]. La sección A(x) está producida por el plano a perpendicular a OX .
Siguiendo un proceso similar al realizado en la definición de la integral de Riemann:
Elegimos una partición regular de [a,b]:
Estas divisiones determinan en el sólido n secciones o rodajas cuya suma se aproxima al volumen del mismo. Teniendo en cuenta que el volumen de un cilindro es R2 , la suma de Riemann asociada a la partición, y que da un volumen aproximado del sólido es:
siendo:
Por tanto, recordando la definición de integral definida de Riemann se obtiene que:
Para hallar el volumen de un sólido por el método de las secciones, se procede como se indica a continuación:
1. Esbozar la figura, incluyendo un eje perpendicular a las secciones de área conocida (es decir, un eje OX)
2. Escoger una sección perpendicular al eje OX.
3. Expresar el área A (x) de la base de la sección en términos de su posición x sobre el eje OX.
4. Integrar entre los límites apropiados.
4. Volúmenes de revolución: Método de capas
En esta sección estudiamos un método alternativo para el cálculo de un volumen de un sólido de revolución,
un método que emplea capas cilíndricas.
Para introducir el método de capas, consideramos un rectángulo representativo, donde:
la capa, viene dado por la diferencia:
Para calcular el volumen de un sólido de revolución con el método de capas, se usa una de las dos siguientes opciones:
1. Esbozar la región plana que va a ser girada, hallando los puntos de intersección de las curvas que la limitan.
2. Sobre el dibujo hallar un rectángulo paralelo al eje de revolución.
3. Teniendo como base el boceto, escribir el volumen de la capa.
4. Integrar entre los límites apropiados.
Observación: Los método de discos y de capas se distinguen porque en el de discos el rectángulo representativo es siempre perpendicular al eje de giro, mientras que en el de capas es paralelo.
Con frecuencia uno de los dos métodos es preferible al otro.
Cálculo de longitudes:
Volumen del disco =
Para ver cómo usar el volumen del disco para calcular el volumen de un sólido de revolución general, consideremos una función continua f (x ) definida en el intervalo [a,b], cuya gráfica determina con las rectas x = a, x = b, y = 0, el recinto R. Si giramos este recinto alrededor del eje OX , obtenemos un sólido de revolución.Se trata de hallar el volumen de este cuerpo engendrado por R. Para ello hay que seguir un proceso similar al realizado en la definición de integral definida.
Elegimos una partición regular de [a, b]:
Estas divisiones determinan en el sólido n discos cuya suma se aproxima al volumen del mismo. Teniendo en cuenta que el volumen de un disco es , la suma de Riemann asociada a la partición, y que da un volumen aproximado del sólido es:
siendo:
- , la altura (anchura) de los cilindros parciales
- el radio de los cilindros parciales
Por tanto, recordando la definición de integral definida de Riemann se obtiene que:
Además, si se toma el eje de revolución verticalmente, se obtiene una fórmula similar:
2. Volúmenes de revolución: El Método de las arandelas
El método de los discos puede extenderse fácilmente para incluir sólidos de revolución con un agujero, reemplazando el disco representativo por una arandela representativa. La arandela se obtiene girando un rectángulo alrededor de un eje. Si R y r son los radios externos e internos de la arandela, y es la anchura de la arandela, entonces el volumen viene dado por:
Volumen de la arandela =
Entonces, generalizando de forma análoga como se hizo en el método de los discos, si tenemos dos funciones continuas f (x) y g (x) definidas en un intervalo cerrado [a,b] con 0" g(x) " f(x), y las rectas x = a, y x = b, el volumen engendrado se calcula restando los sólidos de revolución engendrados por los recintos de ambas funciones, es decir:Si las funciones se cortan, habrá que calcular los volúmenes de los sólidos engendrados en cada uno de los subintervalos donde se puede aplicar el método anterior.
3. Método de secciones conocidas
En este apartado veremos cómo se calcula el volumen de algunos cuerpos geométricos cuando conocemos el área de las bases de los cilindros parciales en que hemos dividido el sólido. Con el método de discos, podemos hallar el volumen de un sólido que tenga una sección circular cuya área sea A = R2. Podemos generalizar este método a sólidos de cualquier forma siempre y cuando sepamos la fórmula del área de una sección arbitraria, como cuadrados, rectángulos, triángulos, semicírculos y trapecios.
Consideremos un sólido que tiene la propiedad de que la sección transversal a una recta dada tiene área conocida. Esto equivale a decir intuitivamente que en cada corte que hacemos, conocemos el área de la sección correspondiente.
En particular, supongamos que la recta es el eje OX y que el área de la sección transversal está dada por la función A(x), definida y continua en [a,b]. La sección A(x) está producida por el plano a perpendicular a OX .
Siguiendo un proceso similar al realizado en la definición de la integral de Riemann:
Elegimos una partición regular de [a,b]:
Estas divisiones determinan en el sólido n secciones o rodajas cuya suma se aproxima al volumen del mismo. Teniendo en cuenta que el volumen de un cilindro es R2 , la suma de Riemann asociada a la partición, y que da un volumen aproximado del sólido es:
siendo:
- Siendo ci un punto intermedio del intervalo [xi-1,xi]
- = xi -xi-1, la altura de los cilindros parciales
- R2 = A(ci) el área de la base de los cilindros parciales
Por tanto, recordando la definición de integral definida de Riemann se obtiene que:
Para hallar el volumen de un sólido por el método de las secciones, se procede como se indica a continuación:
1. Esbozar la figura, incluyendo un eje perpendicular a las secciones de área conocida (es decir, un eje OX)
2. Escoger una sección perpendicular al eje OX.
3. Expresar el área A (x) de la base de la sección en términos de su posición x sobre el eje OX.
4. Integrar entre los límites apropiados.
4. Volúmenes de revolución: Método de capas
En esta sección estudiamos un método alternativo para el cálculo de un volumen de un sólido de revolución,
un método que emplea capas cilíndricas.
Para introducir el método de capas, consideramos un rectángulo representativo, donde:
- = anchura del rectángulo (espesor).
- h = altura del rectángulo.
- p = distancia del centro del rectángulo al eje del giro (radio medio).
la capa, viene dado por la diferencia:
Volumen de la capa = volumen del cilindro - volumen del agujero=
= 2 ph = 2 (radio medio)(altura)(espesor)
Usamos esta fórmula para calcular el volumen de un sólido de revolución como sigue. Suponemos que la región plana gira sobre una recta y engendra así dicho sólido. Si colocamos un rectángulo de anchura y paralelamente al eje de revolución, entonces al hacer girar la región plana en torno al eje de revolución, el rectángulo genera una capa de volumen: V = 2 [p(y)h(y)] y
Si aproximamos el volumen del sólido por n de tales capas de anchura y, altura h( yi), y radio medio p( yi ), tenemos:volumen del sólido =
Tomando el límite cuando n!", tenemos que:Volumen del sólido =
Por tanto, podemos enunciar el método de capas de la siguiente forma:Para calcular el volumen de un sólido de revolución con el método de capas, se usa una de las dos siguientes opciones:
Eje horizontal de revolución:
Eje vertical de revolución:
Para hallar el volumen de un sólido por el método de capas, se procede como se indica a continuación.1. Esbozar la región plana que va a ser girada, hallando los puntos de intersección de las curvas que la limitan.
2. Sobre el dibujo hallar un rectángulo paralelo al eje de revolución.
3. Teniendo como base el boceto, escribir el volumen de la capa.
4. Integrar entre los límites apropiados.
Observación: Los método de discos y de capas se distinguen porque en el de discos el rectángulo representativo es siempre perpendicular al eje de giro, mientras que en el de capas es paralelo.
Con frecuencia uno de los dos métodos es preferible al otro.
Cálculo de longitudes:
longitud de revolución =
longitud de revolución entre funciones =
lunes, 27 de junio de 2011
Longitud de Curvas
La longitud de una curva plana se puede aproximar al sumar pequeños segmentos de recta que se ajusten a la curva, esta aproximación será más ajustada entre más segmentos sean y a la vez sean lo más pequeño posible.
Definición:
Si la primera derivada de una función es continua en [a,b] se dice que es suave y su gráfica es una curva suave.

Cuando la curva es suave, la longitud de cada pequeño segmentos de recta se puede calcular mediante el teorema de Pitágoras y (dL)2=(dx)2+(dy)2, de tal forma que sumando todos los diferenciales resulta:
Definición:
Si f es suave en [a,b], la longitud de la curva de f(x) desde a hasta b es:

http://www.mitecnologico.com/Main/LongitudDeCurvas
lunes, 6 de junio de 2011
Serie Finita criterio D'Alembert y Cauchy
En matemáticas, una serie es la suma de los términos de una sucesión. Se representa una serie con términos an como  donde n es el índice final de la serie. Las series infinitas son aquellas donde i toma el valor de absolutamente todos los números naturales, es decir,
donde n es el índice final de la serie. Las series infinitas son aquellas donde i toma el valor de absolutamente todos los números naturales, es decir, 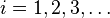 .
.
Las series convergen o divergen. En cálculo, una serie diverge si no existe o si tiende a infinito; puede converger si
no existe o si tiende a infinito; puede converger si  para algún
para algún  .
.
 , tal que ak > 0 ( serie de términos positivos).
, tal que ak > 0 ( serie de términos positivos).
Si existe
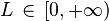 , el Criterio de D'Alembert establece que:
, el Criterio de D'Alembert establece que:
 , tal que ak > 0 (serie de términos positivos). Y supongamos que existe
, tal que ak > 0 (serie de términos positivos). Y supongamos que existe
Wikipedia La enciclopedia Libre
 donde n es el índice final de la serie. Las series infinitas son aquellas donde i toma el valor de absolutamente todos los números naturales, es decir,
donde n es el índice final de la serie. Las series infinitas son aquellas donde i toma el valor de absolutamente todos los números naturales, es decir, 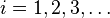 .
.Las series convergen o divergen. En cálculo, una serie diverge si
 no existe o si tiende a infinito; puede converger si
no existe o si tiende a infinito; puede converger si  para algún
para algún  .
.Criterio de D'Alembert o Criterio del Cociente (Criterio de la razón)
Sea una serie , tal que ak > 0 ( serie de términos positivos).
, tal que ak > 0 ( serie de términos positivos).Si existe
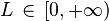 , el Criterio de D'Alembert establece que:
, el Criterio de D'Alembert establece que:- si L < 1, la serie converge.
- si L > 1, entonces la serie diverge.
- si L = 1, no es posible decir algo sobre el comportamiento de la serie.
Criterio de Cauchy (raíz enésima)
Artículo principal: Criterio de la raíz
Sea una serie  , tal que ak > 0 (serie de términos positivos). Y supongamos que existe
, tal que ak > 0 (serie de términos positivos). Y supongamos que existe![\lim_{k \rightarrow \infty} \sqrt [k] {a_k}=L](http://upload.wikimedia.org/math/9/f/9/9f9c8260d0ee84308bde583dc2ca8991.png) , siendo
, siendo 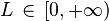
- L < 1, la serie es convergente.
- L > 1 entonces la serie es divergente.
- L=1, no podemos concluir nada a priori y tenemos que recurrir al criterio de Raabe, o de comparación, para ver si podemos llegar a alguna conclusión.
Wikipedia La enciclopedia Libre
miércoles, 1 de junio de 2011
Serie de Potencias
Muchos problemas matem´aticos, f´ısicos, econ´omicos, etc. convienen expresarlos
como suma de una serie de potencias. Este recurso es especialmente ´util en
los casos en los que la funci´on no es elemental; al disponer de su representaci´on
en series de potencias, es posible analizarla, estudiando sus propiedades y su
comportamiento.
Definiciones y propiedades basicas
Definicion. Se llama serie de potencias a una serie funcional de la forma
∑_(n=0)^∞▒anXn
siendo an y x numeros reales.
Como vemos, en cierto modo, una serie de potencias consiste en una especie
de “polinomio con infinitos terminos”.
Ejemplos de series de potencias
• La serie geométrica ∑_(n=0)^∞▒x^n es una serie de potencias absolutamente convergente
si |x| < 1 y no convergente si |x| ≥1. Nota. Usar el criterio del cociente. La serie de potencias ∑_(n=1)^∞▒(x¦n)n es absolutamente convergente para todo ×⋲lR Nota. Usar el criterio de la raız. La serie de potencias ∑_(n=0)^∞▒〖(nx)〗^n solamente converge para x = 0. Serie de potencias Σ anxn Determinación del radio de convergencia R D'Alembert: L = lim |an+1/an| Cauchy: n __ L = \|an L distinto de 0 => R = 1/L
L = +inf => R = 0
L = 0 => R = +inf
D ? C ? D
-----|-----|-----
-R R
Se debe clasificar en x=R y x=-R
http://www.itescam.edu.mx/principal/sylabus/fpdb/recursos/r44024.PDF
Cuando las leyes de la matemática se refieren a la realidad, no son ciertas; cuando son ciertas, no se refieren a la realidad.
como suma de una serie de potencias. Este recurso es especialmente ´util en
los casos en los que la funci´on no es elemental; al disponer de su representaci´on
en series de potencias, es posible analizarla, estudiando sus propiedades y su
comportamiento.
Definiciones y propiedades basicas
Definicion. Se llama serie de potencias a una serie funcional de la forma
∑_(n=0)^∞▒anXn
siendo an y x numeros reales.
Como vemos, en cierto modo, una serie de potencias consiste en una especie
de “polinomio con infinitos terminos”.
Ejemplos de series de potencias
• La serie geométrica ∑_(n=0)^∞▒x^n es una serie de potencias absolutamente convergente
si |x| < 1 y no convergente si |x| ≥1. Nota. Usar el criterio del cociente. La serie de potencias ∑_(n=1)^∞▒(x¦n)n es absolutamente convergente para todo ×⋲lR Nota. Usar el criterio de la raız. La serie de potencias ∑_(n=0)^∞▒〖(nx)〗^n solamente converge para x = 0. Serie de potencias Σ anxn Determinación del radio de convergencia R D'Alembert: L = lim |an+1/an| Cauchy: n __ L = \|an L distinto de 0 => R = 1/L
L = +inf => R = 0
L = 0 => R = +inf
D ? C ? D
-----|-----|-----
-R R
Se debe clasificar en x=R y x=-R
http://www.itescam.edu.mx/principal/sylabus/fpdb/recursos/r44024.PDF
Cuando las leyes de la matemática se refieren a la realidad, no son ciertas; cuando son ciertas, no se refieren a la realidad.
lunes, 30 de mayo de 2011
4.5 Radio de convergencia
En matemáticas, según el teorema de Cauchy-Hadamard, el radio de convergencia de una serie de la forma  , con
, con  , viene dado por la expresión:
, viene dado por la expresión:
EJEMPLO:
 .
.
(para el cálculo de la serie vea serie de Taylor). Su radio de convergencia es r = 1. Eso significa que para calcular si tomo cualquier valor cuya distancia al x0 = 0 es menor que r = 1, por ejemplo el x = 0.25, entonces al remplazarlo en la serie el resultado de calcular la serie será el mismo que remplazarlo en la función, de hecho
 .
.
(la cuenta se puede hacer por serie de potencia). Y por otro lado
 .
.
Pero si tomamos un elemento fuera del radio de convergencia, por ejemplo el x = 2, los más probable es que al remplazarlo en la serie, ésta diverja (por eso el nombre de radio de convergencia). Efectivamente:
 .
.
Wikipedia, la Enciclopedia libre.
 , con
, con  , viene dado por la expresión:
, viene dado por la expresión:EJEMPLO:
Radio de convergencia finito
La función 1 / (1 − x) en su desarrollo con centro 0, o sea, en series de potencia x − x0 = x − 0 = x, tiene el siguiente aspecto: .
.(para el cálculo de la serie vea serie de Taylor). Su radio de convergencia es r = 1. Eso significa que para calcular si tomo cualquier valor cuya distancia al x0 = 0 es menor que r = 1, por ejemplo el x = 0.25, entonces al remplazarlo en la serie el resultado de calcular la serie será el mismo que remplazarlo en la función, de hecho
 .
.(la cuenta se puede hacer por serie de potencia). Y por otro lado
 .
.Pero si tomamos un elemento fuera del radio de convergencia, por ejemplo el x = 2, los más probable es que al remplazarlo en la serie, ésta diverja (por eso el nombre de radio de convergencia). Efectivamente:
 .
.Wikipedia, la Enciclopedia libre.
viernes, 27 de mayo de 2011
evaluacion 4.6
Por medio de la presente informo que el equipo obtuvo el 100%
Atentamente
Ing.Enrique Marquez.
Atentamente
Ing.Enrique Marquez.
4.5 Serie de Taylor
Fórmula de Taylor
Sea f(x) una función definida en un intervalo que contiene al punto a, con derivada de todos los órdenes.
Sea f(x) una función definida en un intervalo que contiene al punto a, con derivada de todos los órdenes.
El polinomio de primer grado p1(x) = f(a) + f ' (a) (x-a) tiene el mismo valor que f(x) en el punto x=a y también, como se comprueba fácilmente, la misma derivada que f(x) en este punto. Su gráfica es una recta tangente a la gráfica de f(x) en el punto a.
Es posible elegir un polinomio de segundo grado, p2(x) = f(a) + f ' (a) (x-a) + ½ f ' ' (a) (x-a)2, tal que en el punto x=a tenga el mismo valor que f(x) y valores también iguales para su primera y segunda derivadas. Su gráfica en el punto a se acercará a la de f(x) más que la anterior. Es natural esperar que si construimos un polinomio que en x=a tenga las mismas n primeras derivadas que f(x) en el mismo punto, este polinomio se aproximará más a f(x) en los puntos x próximos a a. Así obtenemos la siguiente igualdad aproximada, que es la fórmula de Taylor:f(x) ≈ f(a) + f '(a) (x-a) + (1/2!) f ' '(a) (x-a)2 + ...... + (1/n!) f (n)(a) (x-a) n
El resto tiene la peculiaridad de que la derivada que en él aparece debe calcularse en cada caso, no en el punto a, sino en un punto c convenientemente elegido, desconocido, pero interior al intervalo de extremos a y x.
La demostración de la igualdad anterior es bastante engorrosa, aunque sencilla en esencia.Las leyes naturales pueden expresarse, por regla general, con buena aproximación por funciones derivables un número arbitrario de veces, y por ello pueden ser aproximadas por polinomios cuyo grado viene determinado por la precisión deseada.
La fórmula de Taylor, que abre el camino para la mayoría de los cálculos en el análisis aplicado, es muy importante desde el punto de vista práctico.
La idea de aproximar una función mediante polinomios o de representarla como suma de un número finito de funciones más sencillas alcanzó un gran desarrollo en el análisis, donde constituye ahora una rama independiente: la teoría de la aproximación de funciones.
En las siguientes escenas podemos observar cómo la gráfica de las funciones se va "tapando" con la gráfica del polinomio de Taylor al aumentar el grado del polinomio. Para un valor de x calculamos la diferencia entre el valor real y el valor del polinomio correspondiente. Al aumentar el grado del polinomio esa diferencia es cada vez menor. Hemos calculado los polinomios de Taylor para a=0.
1.- Aproximación de la función y = sen (x)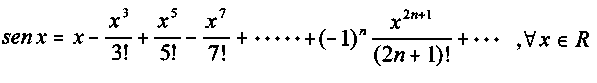
La función p(x)=a0+a1x+a2x2+..........+anxn, en la que los coeficientes ak son constantes, se llama polinomio de grado n. En particular y=ax+b es un polinomio de primer grado e y=ax2+bx+c es un polinomio de segundo grado. Los polinomios pueden considerarse las funciones más sencillas de todas. Para calcular su valor para una x dada, necesitamos emplear únicamente las operaciones de adición, sustracción y multiplicación; ni siquiera la división es necesaria. Los polinomios son funciones continuas para todo x y tienen derivadas de cualquier orden. Además la derivada de un polinomio es también un polinomio de grado inferior en una unidad, y las derivadas de orden n+1 y superiores de un polinomio de grado n son nulas.
Si a los polinomios añadimos las funciones de la forma y=p(x)/q(x) (cociente de polinomios, para cuyo cálculo necesitamos también de la división), las funciones raíz cuadrada de x y raíz cúbica de x, y finalmente, las combinaciones aritméticas de los tipos anteriores, obtenemos esencialmente las funciones cuyos valores pueden calcularse por métodos aprendidos en el bachillerato.
A este nivel se tienen nociones de algunas otras funciones tales como log(x), sen(x), ex, ..., pero, aunque se estudian sus propiedades más importantes, no se da una respuesta a las preguntas: ¿Cómo calcularlas? ¿Qué clase de operaciones, por ejemplo, es necesario realizar sobre la x para obtener log(x) o sen(x)?. La respuesta a estas preguntas la proporcionan los métodos desarrollados por el análisis matemático. Examinemos uno de estos métodos.
Fuente: http://recursostic.educacion.es/descartes/web/materiales_didacticos/Desarrollo_serie_taylor/Desarrollo_en_serie_de_taylor.htm
miércoles, 25 de mayo de 2011
4.6 Representacion de funciones por serie Taylor
En matemáticas, una serie de Taylor de una función f(x) infinitamente derivable (real o compleja) definida en un intervalo abierto (a-r, a+r) se define como la siguiente suma:
Aquí, n! es el factorial de n y f (n)(a) indica la n-ésima derivada de f en el punto a.
Si esta serie converge para todo x perteneciente al intervalo (a-r, a+r) y la suma es igual a f(x), entonces la función f(x) se llama analítica. Para comprobar si la serie converge a f(x), se suele utilizar una estimación del resto del teorema de Taylor. Una función es analítica si y solo si se puede representar con una serie de potencias; los coeficientes de esa serie son necesariamente los determinados en la fórmula de la serie de Taylor.
Si a = 0, a la serie se le llama serie de Maclaurin.
Esta representación tiene tres ventajas importantes:
- La derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales.
- Se puede utilizar para calcular valores aproximados de la función.
- Es posible demostrar que, si es viable la transformación de una función a una serie de Taylor, es la óptima aproximación posible.
Wikipedia, la enciclopedia libre.
lunes, 23 de mayo de 2011
Area bajo la grafica de una funcion
En matematica, la integracion de una funcion no negativa, en el caso más simple, puede ser mirada como el área bajo la gráfica de una curva y el eje x. La Integral de Lebesgue es una construcción matemática que extiende el concepto de integración a una clase mucho más amplia de funciones, así como extiende los posibles dominios en las cuales estas integrales pueden ser definidas. Hace mucho que se sabe que para funciones no negativas con una curva suficientemente suave (como una funcion continua en intervalos cerrados) el área bajo la curva podía ser definida como la integral y calculada usando técnicas de aproximación de la región a través de rectángulos o polígonos. De todas maneras, como se necesitaba considerar funciones más irregulares (por ejemplo, como resultado de los limitados procesos del Cálculo o de la Teoría de Probabilidades), se hizo evidente que una aproximación más cuidadosa era necesaria para definir una integral que se ajustara a dichos problemas.
La integral de Lebesgue tiene un importante rol en el Análisis Real, y en muchas otras ramas de la Matemática. Su nombre es en honor a su creador, Henri Lebesgue (1875-1941).
A continuacion presentamos 2 videos donde se muestra el como obtener el Area bajo la grafica de una funcion por medio de las sumas de Riemann
miércoles, 18 de mayo de 2011
Integral por partes Video
Aqui podemos ver un tutorial sobre la realizacion de una integral por partes de un logaritmo.
Suscribirse a:
Entradas (Atom)